This post is also available in: English (英語)
概要
対比的信頼性伝播 (CCP) アルゴリズムは、パロアルトネットワークスの AI リサーチャーによって開発された、半教師あり学習 (SSL) に対するこれまでにはないアプローチです。このアプローチは、不均衡でノイズの多いラベル付き/ラベルなしデータを使ったモデルのタスク パフォーマンスを向上させます。本稿は、The 38th Annual AAAI Conference on Artificial Intelligence (AAAI '24) にて出版/発表された私たちの論文をもとにしています。本論文は、いくつかの最先端の SSL アルゴリズムとの比較で、 現実世界のデータセットでよく見られる 5 つの異なるデータ品質問題に対する堅牢性を、CCP が拡張することを示しています。
この研究は、専門家がそうした品質に問題のあるデータセットを使って分類器を構築する上で役に立ちます。これにより、ラベルなしデータの有用性を引き出すことができます。ラベルなしデータの方が豊富に存在し、タスクとの関連性も高いことが多いですが、そうしたデータは、クリーンなデータセットでしか機能が実証されていない既知の方法で利用するには汚すぎる可能性があります。
ここでは本論文の概要のほか、機械学習 (ML) を援用するデータ損失防止 (DLP) のサイバーセキュリティ重要タスクに CCP を適用する例を示します。現実世界の DLP のトラフィックはノイズが多く、プライバシー上の懸念から表示できないため、CCP 独自の利点を示すのに最適です。具体的には、私たちは機微なテキスト文書とそうでないテキスト文書を区別する ML 分類器の構築にフォーカスしています。このモデルは、ある機微な文書にどのような機密データが含まれているか (医療情報、財務会計文書、訴訟手続き、ソース コードなど) も識別します。私たちは、CCP を DLP のディープ ニューラル ネットワーク (DNN) 分類器に適用する方法について説明します。その後で「キュレーションを経たテスト セットから実世界のデータに移行したさいの分類精度の損失を低減する」という全体的な目標について示します。
パロアルトネットワークスのお客さまは、Cloud-Delivered Enterprise DLP 製品を通じて、本研究内で言及された脅威からより強力に保護されています。
| 関連する Unit 42 のトピック | 機械学習 |
対比的信頼性伝播 (CCP) の概要
本研究における問い
半教師あり学習 (SSL) は「ラベル付きデータ」と「ラベルなしデータ」の両方を使って、単一のモデルをトレーニングします。多くの場合、SSL は分類器 (各サンプルが定義済みクラス セットの中のどのクラスに属するかを決定するモデル) の構築に使われます。
この文脈において「ラベル付きサンプル」とは「そのサンプルがどのクラスに属するかを事前に知っていること」を意味し、「ラベルなしサンプル」は「そのサンプルの属するクラスを事前に知らないこと」を意味します。ただし「ラベルなし」のデータから有用な情報を抽出し、より優れた分類器を構築できることは少なくありません (図 1)。SSL アルゴリズムはまさにそのために設計されています。

ところが、SSL でトレーニングされたモデルのパフォーマンスが、ラベル付きデータのみで訓練された場合 (完全教師あり学習) のパフォーマンスに劣ることはめずらしくありません。
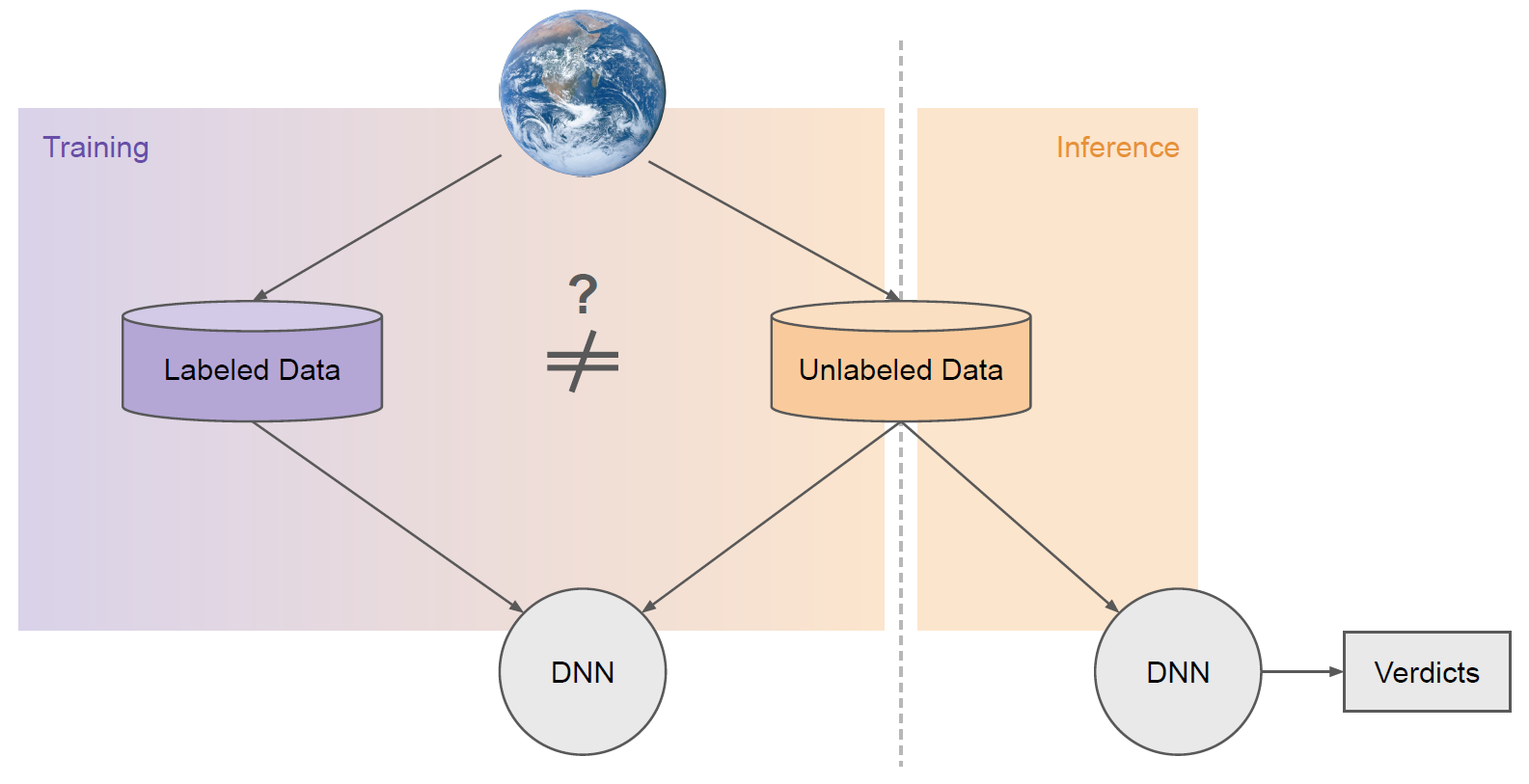
SSL でトレーニングされたモデルのパフォーマンスが劣る理由としてよくあるのが、「ラベル付きデータセットとラベルなしデータセットはそれぞれ異なる特性を持つことが多い」というものです(図 2)。両者は異なるソース (つまり分布) からサンプリングされていることが少なくありません。
たとえば、ラベル付きデータセットは通常、実務者やアノテーション (注釈やラベル) を設定する人たち (アノテーター) がオフラインで手動で収集しています。一方、ラベルなしデータセットは、実世界でのモデルの展開先ソースと同じソースから取得されるのが普通です。
SSL の主目的の 1 つは、ラベル付けするには数が多すぎたり、汚なすぎたりする実世界の分布にモデルを合わせることです。キュレーションを経たラベル付きデータセットは、ラベルなしデータとは異なる特性を持つことがよくあります。
「ラベルなし」という性質上、実世界のデータにおけるクラスの相対度数 (relative frequency) は「不明」であるか、さらには「不可知」であることが多くなります。プライバシー上の懸念や完全自律システムの導入により、ラベルなしデータは表示できないことがあります。
データ品質問題のそのほかの例は次のとおりです。
- クラス内で概念がブレる (クラスの原型となるサンプルからの変化など)
- ラベルなしデータにどのクラスにも属さないデータが含まれている
- 付与されたラベルにエラーがある
SSL アルゴリズムのなかには、こうした品質問題、とくにこれらの問題の組み合わせに対する対処法を備えているものがほとんどありません。文献においてこの点は見過ごされがちです。というのも、多くの研究における唯一の実験変数は、その他の点ではクリーンでバランスのとれた学術データセットに付与されるラベルの数だけだからです。
この私たちの研究における問いは「あらゆるデータセットについて、完全教師ありのベースライン パフォーマンスに匹敵する、ないしそれを上回ることを主目的とする SSL アルゴリズムは構築可能か?」というものです。
コア アルゴリズム コンポーネント
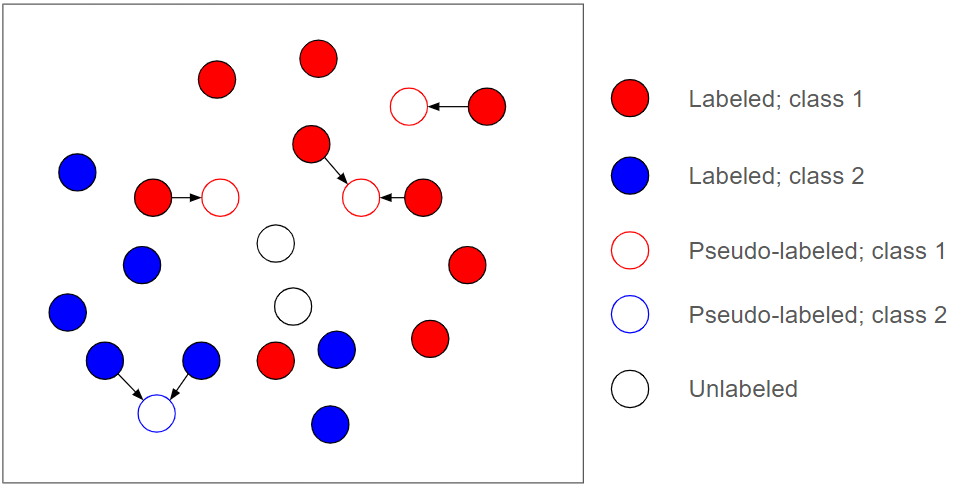
SSL にはさまざまな種類があります。一般的で強力なアプローチは、トレーニング中、「ラベルなしデータ」用にいわゆる疑似ラベルを生成して使うことです。図 3 に示すように、疑似ラベルは、「ラベルなしデータ」に対してトレーニング中に動的に生成される (多くの場合はソフトな) ラベルで、これがその後に行われるトレーニングのための新たな教師用ソースとして使われます。
最良のシナリオでは、すべての疑似ラベルが正しければ、すべての「ラベルなしデータ」が「ラベル付きデータ」と同じくらい強力になります。もちろん、これは非現実的です。
「ラベルなしデータ」の真のクラスは、指定されたラベル情報からは判別できないことがよくあります。つまり、疑似ラベルには必然的にエラーが含まれることから、疑似ラベルのアプローチは本質的に危険を伴うのです。SSL アルゴリズム、とくにディープ ニューラル ネットワークで実装されたアルゴリズムは、疑似的な教師あり学習におけるこれらのエラーに非常に敏感である傾向があります。
本研究課題への取り組みにあたり、私たちはまず単純な仮定から始めました。それは『SSL アルゴリズムが「完全教師あり学習」のベースラインと同等ないしそれ以上のパフォーマンスを発揮できない根本要因は疑似ラベルのエラーである』という仮定です。直感的にいえば、疑似ラベルにエラーがなければ、あるアルゴリズムが少なくとも完全教師あり学習のベースラインと同等のパフォーマンスを出す上でなにも問題は生じないはずです。
対比的信頼性伝播 (CCP) はこの原則に基づいて設計されています。具体的には、必然的に生じる疑似ラベルのエラーに対し、最も堅牢な SSL アルゴリズムを構築することを目指したのです。
反復的な疑似ラベルの精緻化
ノイズの多いラベルを使った機械学習は、盛んに研究がされている分野です。私たちは、CCP に関し、この分野における過去の取り組みからインスピレーションを得ました。
「インスタンス依存」のラベル ノイズと「クラス条件付き」のラベル ノイズとの間には、重要な違いがあります。「インスタンス依存ラベル ノイズ」は、ラベル エラーの確率がそのインスタンスのもつ特定の性質 (特徴) に依存するタイプのノイズを指します。
一方、「クラス条件付きラベル ノイズ」は、真のラベルに依存するタイプのラベル エラーを指します。各疑似ラベルはサンプルごとに動的に生成されることから、疑似ラベルのノイズはインスタンスに大きく依存しています。これにより、私たちの探索範囲はさらに絞り込まれます。
完全教師あり学習の課題においてこれまでに実績のある強力な手法は「SEAL (self-evolution average label: 自己進化平均ラベル)」です。その主な考えかたは、『ノイズの多いラベルを使ってモデルをトレーニングし、そのトレーニング プロセス全体を通じ、データ サンプルごとに複数回、新たな予測を生成する』というものです。次に、それらの予測を平均して、次の反復で使用する次のラベル セットを生成します。これが機能する理由は、誤ったラベルが存在する場合、そのモデルがトレーニング後半で誤ったクラスを記憶する前に、そのモデルの予測が真のクラスと偽のクラスとの間で頻繁に揺れ動くからです。
これらの予測を時間の経過とともに平均化することで、ラベルはゆっくり正しい方向に進みます。私たちの研究でも疑似ラベルの揺れには同様のパターンが見られました。疑似ラベルの揺れの例を図 4 に示します。
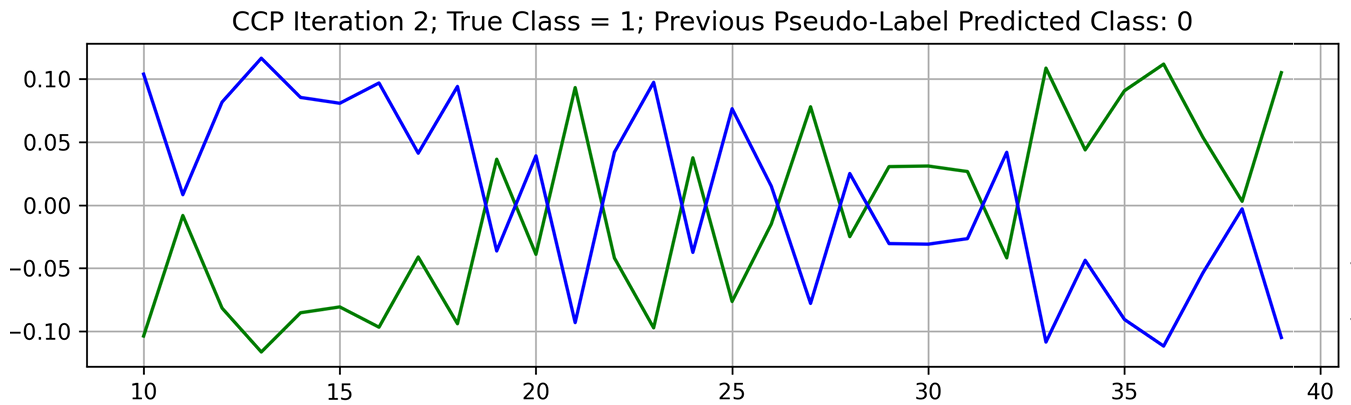
モデルが誤ったラベルにオーバーフィッティング (過学習) していないトレーニングの初期段階は真のクラスのスコアが高くなります。モデルが誤ったラベルに適合する時間があった場合はこれが逆になります。
CCP には、この現象を利用するために設計された外側のループが備わっています (図 5 参照)。トレーニング中のデータ バッチごとに、ラベルなしデータに対して新たな疑似ラベルを予測し、それらを合わせて平均し、それをもって反復の終了とします。
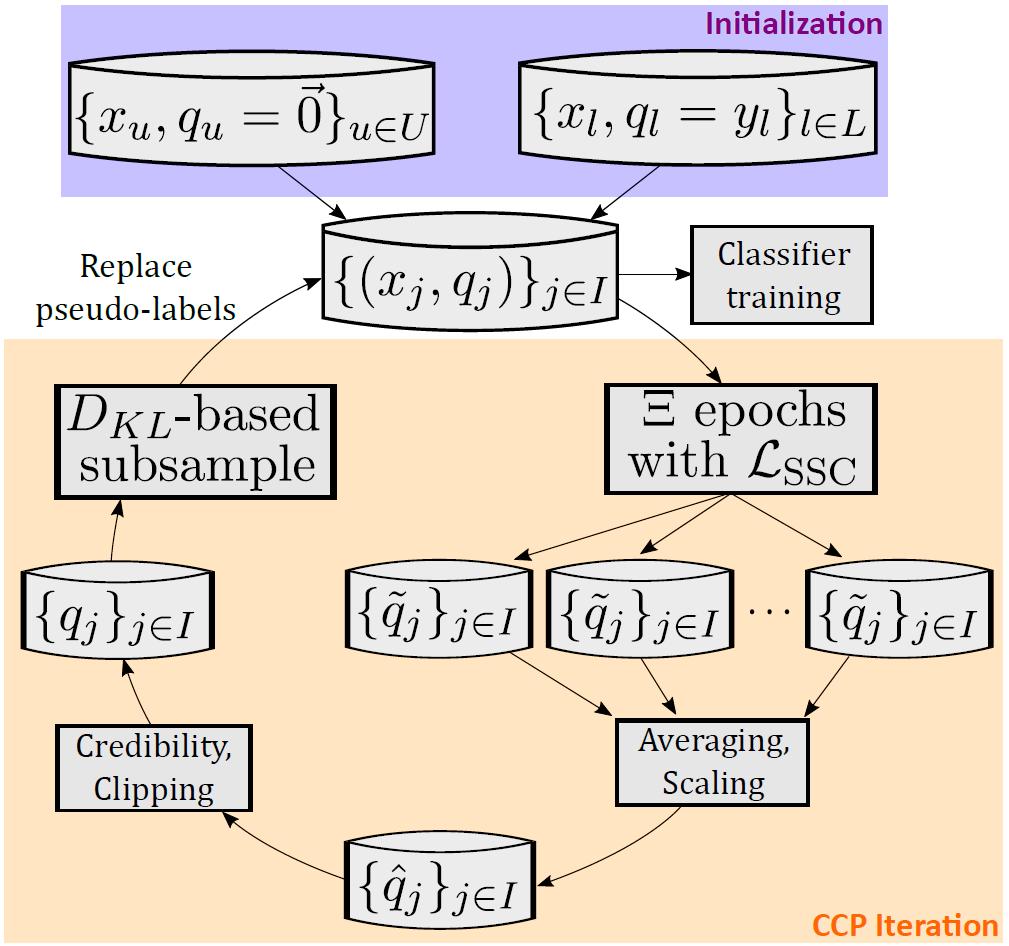
これらの「CCP の反復」は疑似ラベルを反復的に精緻化することを意図したもので、必ず分類器の構築よりも前に実行されます。疑似ラベルはトランスダクティブ (transductive) に生成されます。これはつまり、各サンプルの推測が、バッチ内のほかのサンプルのみに基づいて行われることを意味します。
そして分類器はインダクティブ (inductive: 帰納的) で、すべてのデータをまたいで汎化可能なパターンを学習しようとします。重要なのは、これらのノイズが多くてバッチ レベルでトランスダクティブな疑似ラベルが、私たちのインダクティブな分類器を監督する (supervise) のに直接使われることは決してない、ということです。私たちはまず、反復的な精緻化を通じ、疑似ラベルをクリーン アップします。
信頼性の表現
前述の通り、「ラベルなしデータ」の真のクラスを付与されているラベルのデータから見分けられないことはよくあります。その原因はラベル情報の曖昧さや欠落に求められることがあります。
理想的には、これらのサンプルの疑似ラベル情報は破棄するか、それがだめなら学習への影響をなくしたいところです。私たちはこのうち前者を可能にする「信頼性ベクトル (credibility vector)」と呼ばれるラベル表現を採用しています。
伝統的に、ラベル ベクトルはソフトマックス関数によって計算されます。ソフトマックス関数は、実際の数値のベクトル (クラス スコアまたは類似度) を、すべての成分の和が 1 になり確率として解釈しうる範囲 [0, 1] の値のベクトルへと変換します。
この関数は値の順位を維持します。つまり、小さな入力値は小さな出力値に対応し、大きな入力値は大きな出力値に対応します。信頼性 (credibility) は、[0, 1] という範囲のクラス スコア/類似度の入力ベクトルを、[-1, 1] という範囲の出力ベクトルへと変換します。
信頼性ベクトルにおいて、-1 はクラスとの非類似度に対する高い確信度 (confidence) に対応しています。0 は類似度・非類似度のいずれにも確信度がないことに対応しています。1 はクラス類似度に対する高い確信度に対応しています。信頼性の中心的な考えかたは、クラス類似度の測定値を、次に高いクラス類似度に基づいて条件付けることです (つまり、大きなクラス類似度の測定値が高いままになるのは、ほかにそれほど大きなクラス類似度の測定値がない場合のみとする)。
図 6 の例を考えてみましょう。
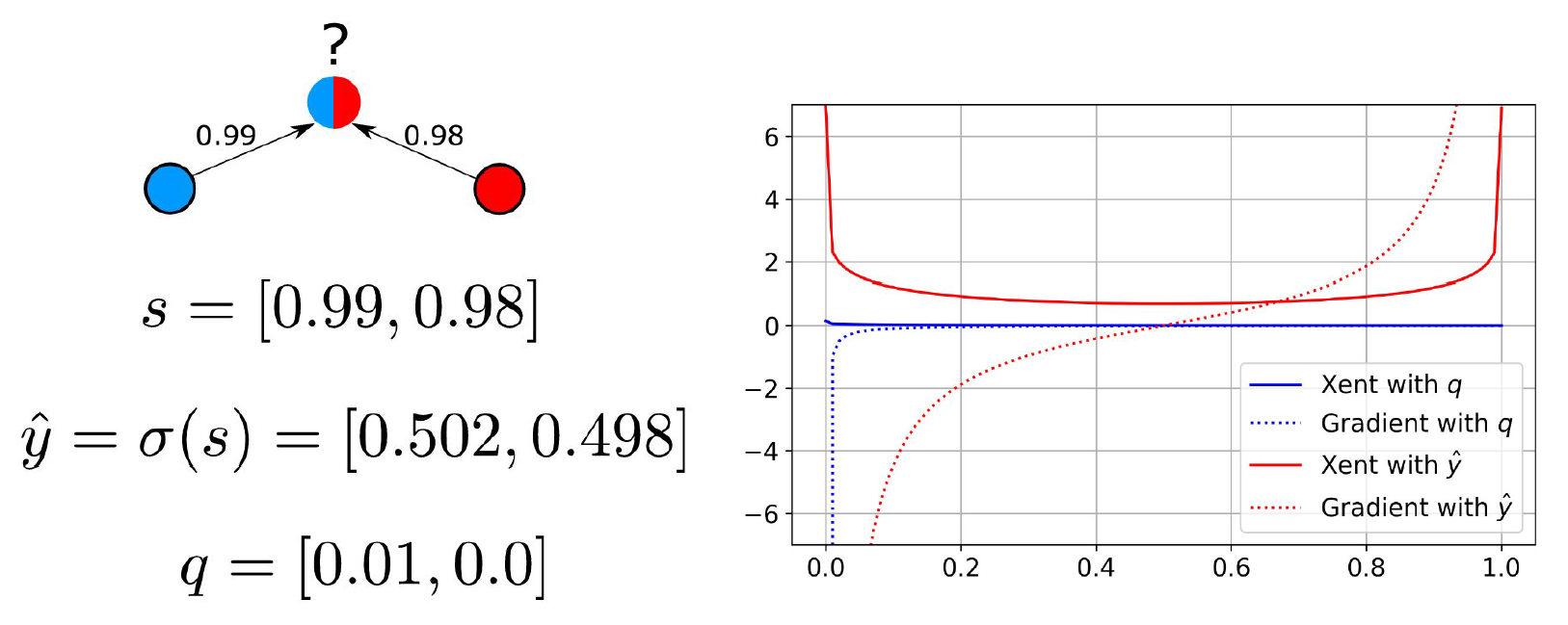
図 6 の左側には、赤クラスと青クラスに対してそれぞれ 0.98 と 0.99 という大きなクラス類似度スコアを持つラベルなしサンプルが表示されています。真のラベルはほぼ曖昧です。ソフトマックス ラベルは [0.502,0.498] と計算されます。信頼性ベクトルは、最初のエントリでは 0.99-0.98=0.01 と計算され、2 番目のエントリでは 0.98-0.99=-0.01 と計算されます (これは 0 にクリッピングされます)。
SSL では、こうした疑似ラベルは分類損失関数を持つ基礎モデルを監視するのによく使われます。交差エントロピー (Xent) と呼ばれる標準的な分類損失関数に対してソフトマックスと信頼性ラベルを使ったさいの効果は図 6 の右側から確認できます。
このプロットでは、X 軸が青クラスに対するバイナリー分類器のソフトマックス出力であるとします。ソフトマックス ラベルを使って交差エントロピーを計算すると、真のクラスがほぼ曖昧であるにもかかわらず、いずれの極でも強い勾配が生じます。
信頼性ラベルを使用すると、このサンプルの勾配が x=0 を除くすべての場所で 0 に近くなることが保証されます。すべてのクラスが同程度の類似度をもつ場合、信頼性ラベルはゼロ ベクトルになり、勾配はどこでもゼロになります。この表現能力は重要です。というのも、例えば真のクラスが識別不能な場合など、サイズを縮小するだけで CCP 反復を通じて誤った疑似ラベルが精緻化される、というのはよくあることだからです 。
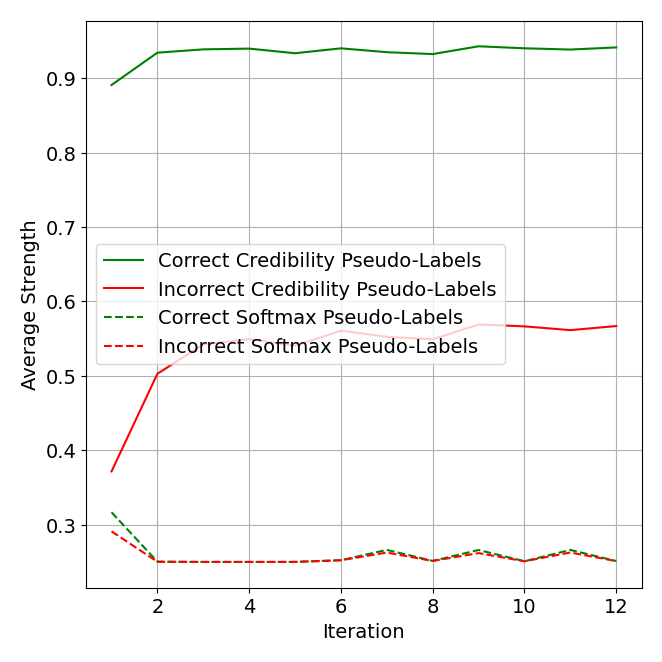
図 7 のアブレーション分析からは、信頼性表現の主な利点が「正しい疑似ラベル」と「誤った疑似ラベル」を区別しうることだと分かります。平均すると、信頼性を使った場合、「正しい疑似ラベル」と「誤った疑似ラベル」との強度 (最大値) 差は、はるかに大きくなります。これは、大きなスコアを割り当てる基準が信頼性ではより厳格であるためと考えられます。したがって、これは確信度 (confidence) を測るより良い尺度となります。
疑似ラベル精緻化から分類器構築まで、CCP のフレームワーク全体が、信頼性 (credibility) とそれが提供するより優れた差別化 (differentiation) をネイティブに活用しています。加重平均を通じ、あるサンプルがラベルの伝播やすべての損失関数に及ぼす影響は、信頼性ラベルの単一の非ゼロ エントリーのサイズに応じて直線的に変化します。零ベクトルは、初回の CCP 反復において、疑似ラベルの自然な初期化も提供します。
サブサンプリング
図 7 は、信頼性ラベルの強度が誤った疑似ラベルの識別に効果的であることを示唆しています。そうなると、このシグナルを使って CCP 反復中に疑似ラベルをさらに精緻化できるのではないか、と思う人もいるでしょう。私たちは、まさにそれを行うサブサンプリング手順を定義しました。
この手順はオプションですが、収束を早めますし、汎化可能な設定でより良いソリューションへと収束するのに役立つこともあります。反復の最後に、最も弱い疑似ラベルの割合を計算して初期状態 (零ベクトル) にリセットします。これにより、ネットワークは次の反復でよりクリーンな疑似ラベル セットをトレーニングできるようになります。リセットされた疑似ラベルには、次の反復で新たな疑似ラベルが割り当てられます。
それでは、最も弱い疑似ラベルの何パーセントをリセットする必要があるのでしょうか。疑似ラベルをたくさんリセットしすぎると、トレーニングが不安定になる可能性があります (つまり疑似ラベルの精度が急速に低下したり反復を通じて収束しなくなったりする)。
私たちは「この不安定性の原因は自己トレーニング (self-training) テクニックで見られる不安定性の原因と似ている」という仮定を立てました。自己トレーニングとは、ラベルなしデータに疑似ラベルを繰り返し割り当て、それら (通常は最も強度の高いデータ) をトレーニング セットに移動していく、という考えかたです。最先端の SSL アルゴリズムの多くは、自己トレーニングの一種として分類できます。
ここで私たちは、さもなくば保持されていたであろう既存の疑似ラベルをリセットしています。つまりある意味でこれは自己トレーニングの逆なのです。
CCP 特有の強みは、サブサンプリングをしなくても非常に安定していることです (これに関する理論的な説明は論文に記載しています)。これにより、「安定性」と「誤った疑似ラベルをリセットしたいという要望」との間でバランスをとる道が開かれます。私たちは、リセット対象となる最も弱い疑似ラベルの候補となるサブサンプリング率を広く検討します。
まず、すべての疑似ラベルの状態を全体的に要約するような、クラス全体の確率分布を計算します (それらをすべて合計してから合計質量で割る)。これが私たちのアンカー分布として機能します。このアンカー分布からの乖離を制限したいわけです。
候補となる各サブサンプリング率について、対応する最も弱い疑似ラベル率をリセットした後、疑似ラベルを全体的に要約する確率分布を再計算していきます。次に、候補となるサブサンプリング率ごとに、新たに要約の確率分布を得ます。
私たちは、候補となる各分布とアンカー分布とのカルバック・ライブラー情報量 (確率分布間の情報の差異) を計算します。これらの乖離尺度 (divergence measures) は、候補となるサブサンプリング率を増加させたとき、要約の確率分布がどの程度変化するかを表します。
サブサンプリングを完了させるさいは、アンカー分布からの乖離がもっとも厳密に制限内に収まっているサブサンプリング率を候補から選択し、単純にその割合を疑似ラベルに適用します。収束をサポートするため、CCP の反復を通じて乖離の厳格な上限を徐々に減らしていきます。
重要なのは、この方法では仮定を課す必要がなく、データセット サイズに合わせて正規化されていることです。したがって、ある単一のサブサンプリング スケジュールは、すべての検証において良好な結果を生みます。
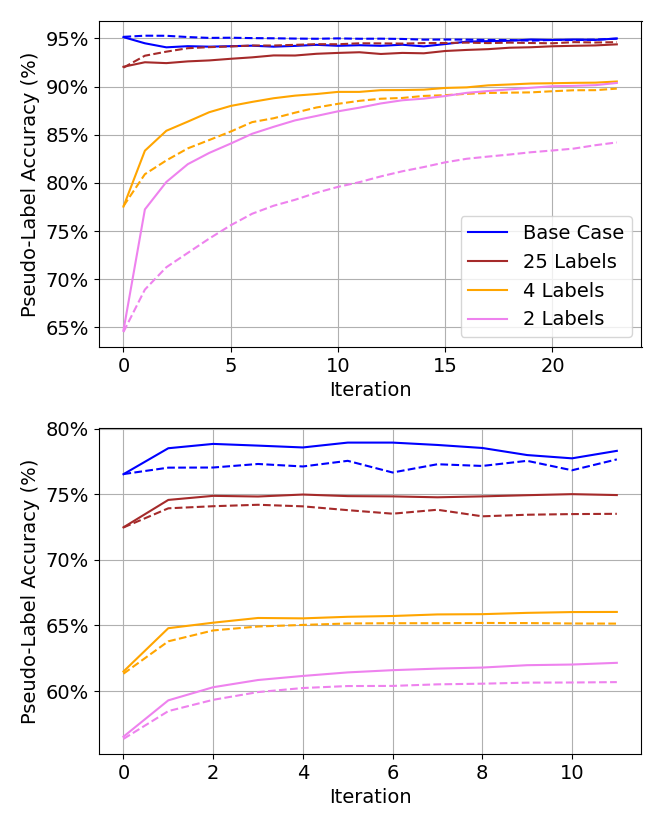
サブサンプリングに関するアブレーション研究の例を図 8 に示します。具体的には、疑似ラベルの状態がより速く収束し、収束時に疑似ラベルの全体的な精度が向上することがわかります。
実験結果
私たちの論文には、全実験結果の包括的概要が記載されています。私たちは、5 種類のデータ品質問題 (データ変数) を列挙し、次にこれらのデータ変数に対する 5 種類の最先端 SSL アルゴリズムの感度を測定します。
感度 (sensitivity) とは、「あるデータ変数が、ある SSL アルゴリズムの結果に対し、どの程度の影響を与えるか」を示すものです。問題となる 5 つのデータ変数は次のとおりです。
- 少数ショット (few-shot): ラベル付きデータの希少性 (scarcity) を変える。
- オープンセット (open-set): どのクラスにも属さないラベルなしデータの割合を変える。
- ノイズラベル (noisy-label): 指定されたラベルのうち誤ったラベルの割合を変える。
- クラス不均衡/不整合 (class imbalance/misalignment): ラベル付きセットとラベルなしセットのクラス頻度分布を別々に変える (ただしもう一方のバランスは保っておく)。
テストされた各アルゴリズムは、単一の特定データ変数に対して最適化されました。しかしここで論じているように、克服すべきデータ変数を実務者が事前に把握していることはまれです。したがって、狭く最適化された方法の実用性にはギャップがあります。
私たちは各データ変数を 3 つの重大度レベルで調査しています。ここでは、CIFAR-10、CIFAR-100 という2 つの標準ベンチマーク コンピューター ビジョン データセット に意図的なノイズ (corruption) を加えることにより、データ変数のシナリオを組み立てています。また、私たちの SSL アルゴリズムのほかに、あらゆるシナリオで教師ありベースラインをトレーニングしています。
簡潔に言えば、CCP は「すべてのシナリオに対する最適なソリューション」というわけではないにせよ、卓越した一貫性を示しました。たとえば、CCP は全シナリオで教師ありベースラインを上回った唯一のアルゴリズムです。
ほかのアルゴリズムについては、いずれも壊滅的なパフォーマンス低下を引き起こすシナリオが 1 つないし複数あることが判明しました。その結果を表 1 に示します。この表はすべてのシナリオに関し、私たちの 2 つのデータセットに対して各アルゴリズムが示した最小精度 (minimum accuracy) を抜き出したものです。
| アルゴリズム | CIFAR-10 | CIFAR-100 |
| CCP (私たちのアルゴリズム) | 90.23% | 61.38% |
| CoMatch | 50.05% | 47.94% |
| ACR | 39.75% | 22.07% |
| OpenMatch | 43.08% | 27.88% |
| FixMatch (データ拡張なし) | 44.62% | 41.84% |
| FixMatch (データ拡張あり) | 46.97% | 40.95% |
表 1. 両データセットのすべてのシナリオにおける各アルゴリズムの最小精度
CCP を DLP に適用
DLP (Data Loss Prevention: データ損失防止) は組織内の機微データを監視してその漏出防止を図る重要なサイバーセキュリティ タスクです。ML を活用する DLP サービスには、特定のドキュメントが機微なものかそうでないのかを自動的に分類するモデルが備わっています。多くの場合、そのモデルはドキュメント内にどんな種類の機微データ (財務、健康、法律、ソース コードなど) が含まれていのるかを判断する必要もあります。
このデモでは、同様のディープラーニング DLP 分類器に CCP を適用しています。話を簡単にするために、入力ドキュメントにはテキストのみが含まれているものと仮定します。ただし、CCP は、あらゆる形式のドキュメントを取り込むタスクを担う、あらゆるモデルに適用されます。このデモ用のドキュメント分類器は、複数の機微ドキュメント クラスと 1 つの非機微クラスを認識します。
こうした分類器の構築に取り組む実務者は、いくつか根本的な課題を克服せねばなりません。定義上、デプロイした環境で分類させたいデータは、プライバシーへの懸念から表示させることができません。
分類器のトレーニング、テスト、検証に使うラベル付きデータセットには、公開された機微文書を集めるか、カスタムで合成したサンプルを使わねばなりません。これらの取り組みはどちらも有用ですが、重要なデプロイメント シナリオでは、ラベル付きデータとプロダクション環境のデータとの間には必然的に大きな情報のギャップが生じます。
クラス度数やコンテンツ度数の分布は大きく異なる可能性があります。また、ある特定クラスの新しいタイプのコンテンツが、プロダクション環境のデータには存在し、ラベル付きデータセットには存在しない可能性があります。当然、実プロダクション環境のデータでトレーニングしたいという要望が生まれます。
CCP を DLP 分類器に適用する概略は次のとおりです。
- ラベルのない機微なプロダクション環境データのプライベート版を抽出する手段を定義する
- CCP のアルゴリズムと損失を計算するために必要となる軽量アーキテクチャ コンポーネントを既存の分類器に追加する
- すべてのラベルなしデータについて CCP の反復を繰り返して疑似ラベル セットを反復的に精緻化する
- 与えられたラベルと疑似ラベルの最終状態を組み合わせて使って最終的な帰納的分類器を訓練する
プライバシーを保護しながら機微データを扱う
プライベート データを使ってトレーニングするためのソリューションは多数提案されています。よく利用されるソリューションには、連合学習 (federated learning)、準同型暗号 (homomorphic encryption)、差分プライバシー (differential privacy、DP) などがあります。
これら技術の比較については本稿の範疇を超えていますので割愛します。その代わり、差分プライバシー (DP) と CCP を組み合わせることで、プライバシーを保護しつつも、効果的に実プロダクション環境のデータをトレーニングする方法について詳しく説明します。
DP がどんなものかを理解するため、以下について想像してみてください。皆さんはある教室にいます。そしてある秘密を抱えています。例えば、好きな食べ物はブロッコリーだけどそれを誰にも知られたくないとしましょう。ここで、先生がクラスの全員の好きな食べ物についてのアンケートを取っているとします。そして皆さんは、嘘をつきたくもないし、誰かに秘密を知られたくもないとします。ここで登場するのが DP です。
皆さんは、本当に好きな食べ物を言う代わりにコインを投げることにします。表が出たら真実を話します。表が出たら、ランダムに食べ物を選びます。
これで、たとえ先生が「クラスにブロッコリーが好きな人がいます」と言ったとしても、それがランダムな選択である可能性があることから、誰もそれがあなたであると確実に知ることはできません。DP はこれと似た働きをします。DP はデータに少しランダムな「ノイズ」を追加します。このノイズは個々の情報をプライベート化するに足りますが、データの全体的な傾向を隠すほどのものではありません。
先生はクラスの生徒の好きな食べ物を大まかに把握することができます。たとえ、密かにブロッコリーが好きなのが皆さんだと知らなくてもです。ここで重要なのは、コイン投げ (またはランダム性) を導入することで、もっともらしい否認の要素が追加されるということです。
たとえ誰かが皆さんがブロッコリーを選んだと推測したとしても、コイン投げによって疑いが生じ、皆さんのプライバシーは保護されます。これを DLP でのドキュメント分類に当てはめて言えば「大規模なドキュメントの集まりにDP を使うことでドキュメント全体の大まかな統計をほぼ保持しながらプロダクション環境のドキュメントのプライバシーは保護する」ということです。
DP ノイズを適用して理論的なプライバシー保証を実現するには、ドキュメントの実数値表現が必要です。この目的には通常、特殊な特徴量抽出モデルが使われます。このモデルの役割は、テキスト ドキュメントを非可逆的な浮動小数点数の大規模な集まりに変換することです。
この表現は人間には判読できませんが、ドキュメントの高レベルのセマンティクス (高められたプライバシー) は保持されます。この浮動小数点表現には、業界標準レベルの DP ノイズが追加され、実プロダクション環境のデータからこの表現を安全に抽出できるようになります。
これで機微文書の表現をプライベート化することはできました。ただしここでさらに、この表現にはラベルがないという事実も克服する必要があります。ここで CCP の出番です。
ニューラル アーキテクチャの詳細
私たちのディープ ラーニング モデルは、ドキュメントをプライベート化した表現を入力として取り込みます。そのタスクは、各入力サンプルに対し、正しい分類の判定を出力することです。
CCP では、独立した埋め込み空間 (embedding space) を定義して、そのなかで入力を比較する類似度関数 (similarity function) を学習する必要があります。この類似度関数は、クラスが異なる入力よりも、クラスが同じで高い類似度を持つ入力を割り当てるようトレーニングされます。
この類似度関数は対比損失関数でトレーニングされ、擬似ラベルをトランスダクティブに生成できるようになります。CCP のコア アーキテクチャ コンポーネントを図 9 に示します。
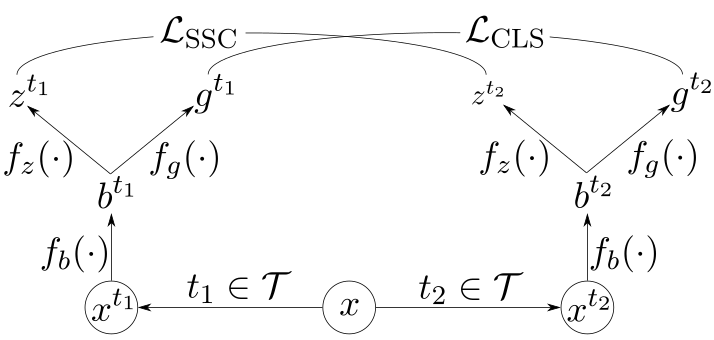
図 9 の表記は次のとおりです。
- \(x\) – 入力サンプル
- \(\mathcal{T}\) – 変換のセット
- \(t\) – 無作為抽出変換
- \(f_b\) – エンコーダー ネットワーク
- \(f_z\) – 対比プロジェクション ヘッド
- \(f_g\) – 分類プロジェクション ヘッド
- \(\mathcal{L}_{\text{SSC}}\) – ソフトな教師あり対比損失関数
- \(\mathcal{L}_{\text{CLS}}\) – 標準的な交差エントロピー分類誤差関数
まず、対比学習に関するほかの研究にならって、私たちはデータに対する変換のセット \(\mathcal{T}\) を定義します。変換の役割は、入力の高レベルでのクラス セマンティクスは維持しつつ、低レベルの詳細に意図的なノイズを加える (corrupt) ことです。
画像であれば、ランダムな切り抜きやカラー ジッターがこの用途に使えるでしょう。テキストであれば、埋め込みベクトル (embedding vector) へのノイズ追加や、単語の無作為な隠蔽などが使えるでしょう。
2 つの変換をランダムに描画すると、同じクラス ラベルを持つ各入力サンプルの 2 つのビューが生成されます。こうした変換は、学習された類似度尺度や分類器が、低レベルのノイズを堅牢に克服するのに役立ちます。
エンコーダー ネットワーク \(f_b\) は、変換済みのデータ バッチを処理します。このエンコーダーの役割は、入力を新しいエンコードされたベクトル空間に変換することです。
\(f_b\) の正確な構造 (CNN、Transformer、RNN など) は、「対象データ型にとって意味があるものは何か」にのみ依存します。DLP や自然言語のドキュメントだと、Transformer が一般的な選択肢となります。
2 つのプロジェクション ヘッド (\(f_z\) and \(f_g\)) は、エンコーダーの出力を 2 つの新しいベクトル空間に取り込み、これらの空間上で損失関数を計算します。各プロジェクション ヘッドは多層パーセプトロン (全結合層の短いシーケンス) です。
既存のディープ ラーニング DLP 分類器に関して言えば、\(f_g\) は分類器の最終層 (ここでソフトマックスと分類損失を計算) となり、\(f_b\) はそれ以前のすべての層となります。類似度尺度の学習に使われる \(f_z\) プロジェクション ヘッドが、追加する唯一の新しいニューラル ネットワーク コンポーネントになります。
類似度尺度の学習と適用
CCP 固有のアルゴリズムと損失は、\(f_z\) で定義されたベクトル空間内で計算されます。私たちは、ソフトな教師ありの類似度尺度の学習のために、これまでにはない対比損失を定義しています。
よく使われている対比損失関数は SimCLR と SupCon の 2 つです。これらは、それぞれ同じ損失関数の教師なし/教師ありバージョンと解釈できます。どちらの損失関数も、「正のペア」と「負のペア」が個別にサンプリングされることを前提としています (それぞれ、「類似するペア」と「類似しないペア」をに対応)。ソフトな疑似ラベルがある場合はそうではありません。私たちは、疑似ラベル ベクトルの大きさが定義する「正のペア」の関係についての変動する確信度だけを持っています。
私たちは、この不確実性に対処するために設計された SimCLR と SupCon の汎化 \(\mathcal{L}_{\text{SSC}}\) について説明します 。私たちの研究は、SimCLR 損失関数と SupCon 損失関数は \(\mathcal{L}_{\text{SSC}}\) の特殊ケースであることを示しています。
図 5 で視覚化したアルゴリズムの形式化に続いて、この学習した類似度尺度を使って疑似ラベルを伝播し、その後はエポック全体で疑似ラベルを平均化するサイクルを繰り返します。必要に応じ、上記で定義したサブサンプリングを適用します。
プロセスが収束したら、疑似ラベルの最終状態を使って、\(f_b\) と \(f_g\) で構成される新たな帰納的分類器をトレーニングします。実際には、分類器のトレーニング中に \(f_z\) を追加損失関数として保持して \(\mathcal{L}_{\text{SSC}}\) を計算すると分類性能が向上します。ただし、推論中は \(f_z\) は破棄されます。
影響
本稿は、CCP を使い、キュレーションされたラベル付きデータセットとラベルなしのプライベート化された本番データの組み合わせで DLP 分類器をトレーニングする手順を概説しました。これは、手元の機械学習モデルを対象プロダクション環境のデータ分布に近づけるための重要な一歩となります。
社内実験のテスト セットでも同様に高い分類パフォーマンスを達成してはいましたが、CCP で調整した DLP 分類器は実環境のテストで機微文書の検出成功率を 250% 向上させました。これは、機械学習モデルを実際のデプロイメント環境のデータ分布と確実に適合させることがいかに重要かを物語るものと言えます。キュレーションされたデータセットのテスト分割における従来のパフォーマンス尺度は、かなり誤解されやすいことがあります。
CCP は、デプロイメント環境のデータ分布がラベルなしである場合や、そもそもデータを表示できない場合でも、自信を持ってモデルを調整するための有用なツールを実践者に提供してくれます。DLP はひとつの実験設定にすぎません。CCP は、部分的なラベル付きデータセット上に構築された、あらゆる分類器に価値を提供できるほど汎用的です。
結論
本稿では、AAAI '24 で発表した CCP アルゴリズム、そのコア コンポーネント、複数のベンチマーク分析について詳細にレビューしました。また、CCP をほかの半教師あり学習アルゴリズムと比較し、前者の具体的かつ独自の利点について論じました。
さらに、DLP に CCP を適用する例について説明しました。DLP はあらゆる企業向けサイバーセキュリティ ソリューションの重要コンポーネントのひとつです。そして私たちは、DLP が CCP 独自の強みを発揮するのに適している理由について論じました。
パロアルトネットワークスは、最先端の DLP を改良し続けています。Enterprise DLP をお使いのお客さまは、CCP を通じ、機微なデータの損失からより強力に保護されています。
追加リソース
- Contrastive Credibility Propagation for Reliable Semi-Supervised Learning – Brody Kutt, Pralay Ramteke, Xavier Mignotar et. al. on arXiv
- A Simple Framework for Contrastive Learning of Visual Representations – SimCLR on GitHub
- Supervised Contrastive Learning – Prannay Khosla, Piotr Teterwak, Chen Wang et al. on arXiv
- Self-Training: A Survey – Massih-Reza Amini, Vasilii Feofanov, Loic Pauletto et al. on arXiv
- Differential Privacy – Wikipedia
- Homomorphic Encryption – Wikipedia
- Federated Learning – Wikipedia
- Kullback-Leibler Divergence – Wikipedia
- Cross-Entropy – Wikipedia
- Softmax Function – Wikipedia
- Statistical Classification – Wikipedia
- Semi-Supervised Learning – Wikipedia
- Data Loss Prevention – Palo Alto Networks
- The 38th Annual AAAI Conference on Artificial Intelligence
- CIFAR-10 and CIFAR-100 – Alex Krizhevsky, Learning Multiple Layers of Features from Tiny Images.
2024-07-02 19:17 JST 英語版更新日 2024-06-28 09:55 PDT の内容を反映してテキストを修正









 Unit 42 からの最新情報を取得
Unit 42 からの最新情報を取得