This post is also available in: English (英語)
概要
LockCryptはEncryptServer2018という別名でも知られるランサムウェアファミリで、2017年の半ばからインターネット上に出回りはじめて以降依然として活発です。このマルウェアはリバースエンジニアリングによる完全な分析を Malwarebytes Labsが2018年4月に行っていますが、利用されている自家製の暗号はお粗末なもので、解読は可能と正しく結論づけています。
ただし、Malwarebytesのリサーチャーは本マルウェア用の復号ツールは公開しておらず、ほかにオンライン上で公開済みの復号ツールも確認できませんでした。また、これ以外にあげられている支援は同ラボの新しいブログエントリしかなく、そこでも同ランサムウェアの被害にあった人はMichael Gillespie (@demonslay335)に復号について相談するよう勧めているのみでした。
そこで私たちはGillepsie氏に連絡を取り、@hasherezade、@FraMauronzの両氏と復号ツールの作成をしましたが、この復号ツールは完全とはいえませんでした。既知の平文ファイル(1MB)が大量に必要でしたし、復元できないファイル名があったり、ファイルの末尾1-2バイト分が復号できずに残る場合があったのです。
これを受け、本稿では、本マルウェアの自家製暗号について分析した結果とその解読方法、また25KB程度のごく小さい平文のみで暗号キーを復元する方法について説明します。このシナリオであれば現実的といえるでしょう。というのも、LockCryptは手当たり次第すべてのファイルを暗号化しますが、DLL のようなアプリケーションファイルもその例外ではないため、同じバージョンのソフトウェアを別のコンピュータにインストールすれば容易に復元可能だからです。復元用スクリプトや手順などは本稿の末尾に記載します。
ただし最近、別の暗号方式を利用する新しい亜種が見つかっている点はご注意ください。私たちはこの新しいバージョンの解析は行っていませんが、こちらはずっと堅牢な暗号が利用されているようです。
初期の分析
このマルウェアの暗号を逆アセンブルしてみてわかったことは、このマルウェアの作成者は、ファイルを暗号化するにあたり、カスタムメイドの非常に弱い暗号を選んだということでした。私たちは、2018年にもなってカスタムメイドの暗号モデルを利用したランサムウェアと遭遇することがあるなどとは思ってもいませんでした。というのも、Windows API を利用すれば、今現在ないし近い将来に利用可能なハードウェアでは復号に数十億年かかるような方式で、簡単にデータを暗号化できるからです(たとえば、十分に暗号強度の高いメソッドを使って生成されたキーを持つ128ビットAES暗号方式など)。
以下に示すのは、本マルウェアの暗号関数を逆アセンブルした結果を同等のPythonコードで示したものです。なお当該encrypt()関数のC言語版はMalwarebyteによる分析に掲載されています。ポインタ操作がある分、こちらの方が分かりやすいかもしれません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
def grouper(iterable, n, fillvalue=None): """returns a generator which iterates iterable in groups of size n. in case the last group is incomplete, it is padded with fillvalue""" args = [iter(iterable)] * n return itertools.izip_longest(fillvalue=fillvalue, *args) def rol(val, n, width): """equivalent to the x86 rol opcode""" return (val << n) & ((1<<width)-1) | \ ((val & ((1<<width)-1)) >> (width-n)) def encrypt(key, plain): size = len(plain)-2 enc = io.BytesIO(plain) # phase 1 key_cyclic = grouper(itertools.cycle(key), 4) for _ in xrange(0, size&(~0x3), 2): # align the size of the data to a multiple of 4 bytes # get the next key dword k = "".join(key_cyclic.next()) k = struct.unpack("<I", k)[0] # get the next data dword d = enc.read(4) d = struct.unpack("<I", d)[0] # XOR them and put it back to the data e = k^d e = struct.pack("<I", e) enc.seek(-4, os.SEEK_CUR) enc.write(e) # go back 2 bytes in the data stream (so that loop iterations overlap) enc.seek(-2, os.SEEK_CUR) # phase 2 enc.seek(0, os.SEEK_SET) key_cyclic = grouper(itertools.cycle(key), 4) for i in xrange(0, size&(~0x3), 4): # get the next key dword k = "".join(key_cyclic.next()) k = struct.unpack("<I", k)[0] # get the next data dword d = enc.read(4) d = struct.unpack("<I", d)[0] # rotate the data dword e = rol(d, 5, 32) # XOR it with the key dword e = e^k # swap the byte order e = struct.pack(">I", e) # put the data dword back enc.seek(-4, os.SEEK_CUR) enc.write(e) return enc.getvalue() def encrypt_file(key, file): # len(key) == 25000 # leave the first 4 bytes as-is file.seek(4, os.SEEK_SET) # encrypt the rest of the first 1MB of the file plain_data = file.read(0x100000 - 4) enc_data = encrypt(key, plain_data) file.seek(4, os.SEEK_SET) file.write(enc_data) # leave the rest of the file as is |
この関数からは以下の結論が導き出せます:
- フェーズ1が定義する変換は周期的で、1サイクルの長さは12500バイト
- フェーズ2が定義する変換は周期的で、1サイクルの長さは25000バイト
- エッジケース(後述)を除き、各平文ビットは3つのキービットとXOR演算される(2つのキーはフェーズ1、残り1つはフェーズ2で)
- つまり、フェーズ2で行われたビット シフトを「取り消す」(バイト順を入れ替え戻した上で5ビット分ROR演算を行う)ことで、両フェーズをひとまとめとし、長さ25000バイトの周期的キーをもつストリーム暗号として扱うことができる(また、それがオリジナルのキーの機能でもある)。
最後の2つの結論について次の図で説明します。この図はデータの4バイト目から8バイト目を変換する様子を、各暗号関数のそれぞれのステップの流れを追って可視化したものです。各行の間にある⊕という記号は、それらのビットが互いにXOR演算されているということを意味しています。
変換が行われる前の4バイト目から8バイト目の各ビットは以下のような状態です:
フェーズ1ループの2回目の繰り返しが終わった後は次のようになります:
フェーズ1ループの3回目の繰り返しが終わった後は次のようになります:
フェーズ1ループの4回目の繰り返しが終わった後は次のようになります(フェーズ1のループはすべて同じことの繰り返し):
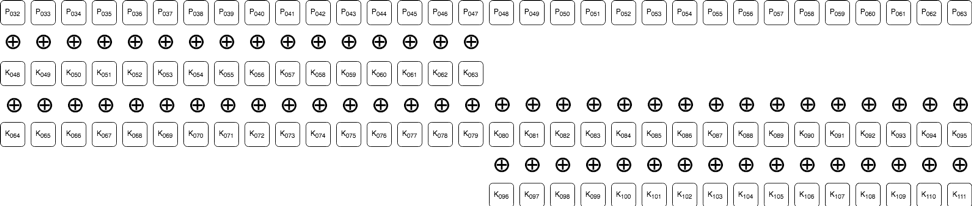
フェーズ2ループの2回目の繰り返し中、ROL演算が終わった後は次のようになります:
フェーズ2ループの2回目の繰り返し中、XOR演算が終わった後は次のようになります:
バイト順を入れ替えてこれらのバイトの暗号化は終了です。
「ストリーム キー」を復元する
先の図で暗号化された4バイト目から8バイト目を使い、バイト順の入れ替えを元に戻して5ビット分ROR演算をすると次の結果が得られます:
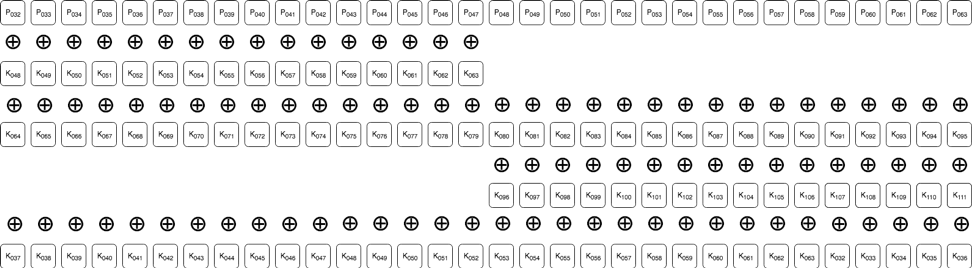
要するに、この演算(バイト順の入れ替えを元に戻して5ビット分ROR演算する)により、この暗号を典型的なストリーム暗号に「正規化」したわけです。この後、これらのバイトと既知の平文とのXOR演算を行えば、先の結論4で述べたキー ビットの機能が得られます:
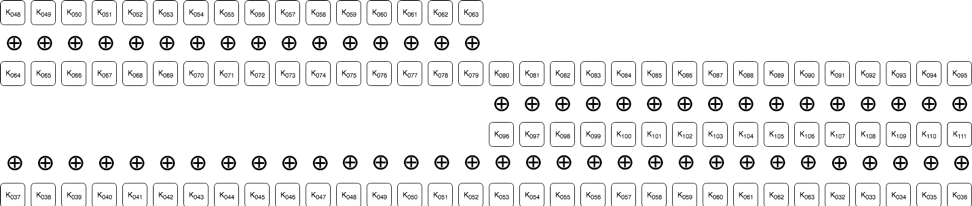
このストリーム(実際には各ビットがキー ビットと3回XOR演算されている)を「ストリーム キー」と呼ぶことにしましょう。このストリームキーは25000バイト長のサイクルで周期性があるので、25000(25k)バイトの長さの平文と暗号文があれば、キーを復元してファイルを復号するのに十分といえそうです。
なにか既知の平文と暗号データのペアを次のPythonの関数で処理すればストリーム キーを復元できます。ここでインデックス パラメータは、与えられた文字列中の25000バイト分の既知の平文バイトに対するインデックスを示しています。ただし、先頭4バイト分は暗号化されることがないため、ここから 4 を引いています。つまり、平文の文字列のインデックスidx+4からidx+4+25000の範囲が使用されます。このため、既知の平文ファイルのサイズが50000バイトなら0 <= idx < 24998の範囲が利用されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
key_len = 25000 def ror(val, n, width): return ((val & ((1<<width)-1)) >> n) | \ (val << (width-n) & ((1<<width)-1)) def recover_stream_key(plain, enc, idx): assert len(plain) == len(enc) assert len(plain) >= 4 + idx + key_len plain = io.BytesIO(plain) enc = io.BytesIO(enc) assert plain.read(4) == enc.read(4) plain.seek(idx & (~3), os.SEEK_CUR) enc.seek(idx & (~3), os.SEEK_CUR) stream_key = io.BytesIO() for i in xrange(0, key_len + (idx % 4), 4): # read the next plain dword p = plain.read(4) p = struct.unpack("<I", p)[0] # read the next encrypted dword and undo the bit shifts on it e = enc.read(4) # unswap the byte order e = struct.unpack(">I", e)[0] # ROR back 5 bits e = ror(e, 5, 32) # XOR the plain and normalized encrypted dwords k = p^e k = struct.pack("<I", k) # write the stream key dword to the recovered stream key stream if i == 0: stream_key.write(k[idx % 4:]) elif i < key_len: stream_key.write(k) else: # i == key_len stream_key.write(k[:-idx % 4]) stream_key = stream_key.getvalue() assert len(stream_key) == key_len return stream_key |
それではいよいよ(まだ不完全ですが)次の関数を使ってファイルを復号していきましょう:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
def decrypt(stream_key, enc): size = len(enc) - 2 plain = io.BytesIO(enc) stream_key_cyclic = grouper(itertools.cycle(stream_key), 4) for i in xrange(0, size&(~3), 4): # read the next stream key dword sk = "".join(stream_key_cyclic.next()) sk = struct.unpack("<I", sk)[0] # read the next encrypted dword and undo the bit shifts on it e = plain.read(4) # unswap the byte order e = struct.unpack(">I", e)[0] # ROR back 5 bits e = ror(e, 5, 32) # XOR the normalized encrypted dword with the stream key dword to recover # the plain dword p = e^sk p = struct.pack("<I", p) plain.seek(-4, os.SEEK_CUR) plain.write(p) return plain.getvalue() def decrypt_file(stream_key, file): assert len(stream_key) == key_len # leave the first 4 bytes as-is file.seek(4, os.SEEK_SET) # decrypt the rest of the first 1MB of the file enc_data = file.read(0x100000 - 4) plain_data = decrypt(stream_key, enc_data) file.seek(4, os.SEEK_SET) file.write(plain_data) # leave the rest of the file as is |
残念ながら、上記のソリューションにはいくつかのエッジケースは扱えていません:
- 暗号化された最初の2バイト(元のファイルの4バイト目から6バイト目)は、2つのキー ビットとしかXOR演算されていないので:
- 残りのバイトを復号するには、idx >= 2 のストリーム キーを使う必要がある
- 最初の2バイトを復号するには、idx == 0 のストリーム キーを使う必要がある
- 元ファイルのサイズが2 (mod 4)に等しくなければ、encrypt()関数にlen(plain) != 0 (mod 4)があることから、ファイルの末尾1-2バイトはフェーズ1の最終の繰り返し回によってしか暗号化されていないことになる。これら末尾1-2バイトの各平文ビットは1つのキービット(得られていないキー ビット)としかXOR演算が行われていないため、復号できない。
さらにMalwarebytesが示したように、ファイル名はオリジナルのキーのサブセットと直接XOR演算して暗号化されているため、ファイル名も復号できません。ただし、@demonslay335 氏が復号ツールの中で使っているように、暗号化されたファイル名の長さをmとした場合、n >= m の長さをもつ既知のファイル名があれば復号は可能です。
つまるところ、任意の長さのファイルとファイル名を復元したければ、本稿で述べたストリーム キーだけでなく、実際のオリジナル暗号キーが必要そうだ、ということです。
オリジナル暗号キーを復元する
実は、これまでの分析から(XORを加算演算とするガロア体(2)上の)連立一次方程式が得られ、ストリーム キーとオリジナル キーをこの方程式で結びつけることができるようになります。この分析を一般化するなら、次のPythonの関数によって、オリジナル キーをそのビット インデックス間でXOR演算した結果が得られ、それが各ストリーム キーのビット(i をインデックスとして使用)が生成されます:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
key_bitlen = 25000*8 def k_for_i(i): i_dword = i >> 5 # the index of the dword for bit i i_offset = i % 32 # the index of bit i in its dword i = i + key_bitlen k = [] k.append((i_dword << 6) + i_offset) if i_offset < 16: k.append(k[0] - 16) else: k.append(k[0] + 16) k.append((i_dword << 5) + ((i_offset + 5) % 32)) return [x % key_bitlen for x in k if x >= 0] |
つまり、stream_key[i] == reduce(xor, (key[k] for k in k_for_i(i))) ということです。
この関数により、ガロア体(2)上に、オリジナル キーとストリーム キー間の変換を表す200000x200000の非常に疎な行列が生成されます:
|
1 2 3 4 5 |
def gen_equations(idx): A_i_j_s = [] for i in xrange(idx << 3, (idx << 3) + key_bitlen): A_i_j_s.append(k_for_i(i)) return A_i_j_s |
この行列Aは、A_i_j_s[i]列だけが1で、残りの行iはすべて0となります。
またこの行列は各行に3つしか値がないという「非常に」疎な行列なので、普通のコンピュータ上で線形代数モデルを使って解くことも可能です。たとえば数学ソフトウェアのSageMathで次のコードを実行させます:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# fix the following parameters to those of your own stream_key_idx = 25000 # the stream key idx you recovered stream_key_path = "key-stream-idx-25000.bin" # the path to the stream key you recovered original_key_path = "key.bin" # the path to write the original key to import itertools import struct def grouper(iterable, n, fillvalue=None): args = [iter(iterable)] * n return itertools.izip_longest(fillvalue=fillvalue, *args) def str2bits(s): bits = [] for dword in grouper(s, 4): dword = "".join(dword) dword = struct.unpack("<I", dword)[0] bits += [(dword >> i) & 1 for i in xrange(32)] return bits def bits2str(bits): s = [] for dword_bits in grouper(bits, 32): dword = 0 for i, bit in enumerate(dword_bits): dword = dword | (bit << i) s.append(struct.pack("<I", dword)) return "".join(s) with open(stream_key_path) as f: stream_key = f.read() assert len(stream_key) == 25000 stream_key_bits = str2bits(stream_key) Y = vector(GF(2), 200000, stream_key_bits) # create a matrix with the equations for the stream key bit A_i_j_s = gen_equations(stream_key_idx) A = matrix(GF(2), 200000, sparse=True) for i, A_i_j in enumerate(A_i_j_s): for j in A_i_j: A[i,j] = 1 # recover the original key bits X = A.solve_right(Y) key_bits = [int(x) for x in X.list()] key = bits2str(key_bits) with open(original_key_path, 'wb') as f: f.write(key) |
検証してみたところ 16GB の RAM を搭載した Intel Core i7-4790 CPU と SageMath 上でこの方程式を数十分から数百分程度で解くことができました。重要なファイルを完全に復元したいなら、これは十分実用的といえるでしょう。なお、idxが25000の倍数であれば、処理が速くなるようです。これは、行列が行階段形に近くなるためかもしれません。したがって、十分に大きい(50KB以上など)既知の平文ファイルがあるならidx = 25000とすることを推奨します。
ファイルを復号する
以上をまとめますと、マルウェアが利用する暗号キーを復元する手順は以下のようになります:
- 暗号化済ファイルについて、暗号化される前の平文ファイルを用意します。この元ファイルは、少なくとも 25006 バイト以上のものが必要です。
- 暗号化前の元ファイルを用意するには、ランサムウェアによって暗号化されたソフトウェアと同じバージョンのソフトウェアを別のコンピュータ上にインストールしてから、ファイルサイズをヒントとして、暗号化された DLL ファイルと対応する平文DLLファイルを探すとよいでしょう。
- まだインストールされていない場合はPython 2.7をインストールします。
- recover_stream_key.pyスクリプトを使い、暗号化されたファイルとそうでないファイルのペアから特定のidx用のストリーム キーを復元します。
- 先に説明したとおり、十分に大きな平文ファイルがあるならidx = 25000にすることをお勧めします。
- SageMathをインストールします。
- SageMath Jupyter Notebookを開き、「オリジナル暗号キーを復元する」セクションに記載されている 3 つのコード スニペットを上から順にペーストしてから実行します(訳注: 日本語版ではコード部分を画像として記載しておりますので、ここでは英語ブログの「Recovering the original key」セクションからコピーすることをおすすめします)。これによりオリジナルの暗号キーを復元します。
- 重要: コード実行前に必ずスニペット上部に記載されている3つのパラメータをご自身のものに書き換えてください。
- 検証によれば、この段階に20分から数時間かかることがあります。
- 本稿末尾のリンクからダウンロードしたdecryptor.pyスクリプトで、暗号化されたファイルを復号します。
本稿の分析とスクリプトファイルが、当該ランサムウェアの被害に遭われた方々の失われたファイルを復元するお役に立てば幸いです。
両スクリプトはこちら のUnit 42チームのGitHubからダウンロードできます。
脅威リサーチ
脅威アクター グループ
主なサイバー脅威
Unit 42 からの最新情報を取得